Strange Paths

Using computer animation¹ based on molecular research² it is possible to see how DNA is actually copied in living cells. This animation shows the “assembly line” of biochemical machines which pull apart the DNA double helix and output a copy of each strand. The DNA to be copied enters the whirling blue molecular machine, called helicase, which spins it as fast as a jet engine as it unwinds the double helix into two strands. One strand is copied continuously, and can be seen spooling off on the other side. Things are not so simple for the other strand, because it must be copied backwards, so it is drawn out repeatedly in loops and copied one section at a time. The end result is two new DNA molecules.

1. Drew Berry, “DNA animation”, The Walter and Eliza Hall Institute of Medical Research, Melbourne, Australia (courtesy of the author). © 2007 Howard Hughes Medical Institute [↩]
2. T. A. Baker, S. P. Bell, “Polymerases and the Replisome: Machines within Machines“, Cell, 92:295-305 (1998); K. P. Lemon, A. D. Grossman, “Movement of Replicating DNA through a Stationary Replisome“, Molecular Cell, 6, 6:1321-1330 (2000); M. R. Singleton, M. R. Sawaua, T. Ellenberger, D. B. Wigley, “Crystal structure of T7 gene 4 ring helicase indicates a mechanism for sequential hydrolysis of nucleotides“, Cell 101:589-600 (2000); D. S. Johnson, L. Bai, B. Y. Smith, S. S. Patel, M. D. Wang, “Single-Molecule Studies Reveal Dynamics of DNA Unwinding by the Ring-Shaped T7 Helicase“, Cell 129, 7:1299-1309 (2007). [↩]

In 1610 Galileo published the astonishing report of his first telescope observations,¹ containing detailed drawings of the moon surface and his discovery of four “planets” orbiting around Jupiter (now known as the “Galilean Moons”). About two years later, he wrote an even more precise observation² with more than a hundred drawings of their relative daily positions. This animation³ brings back life to Galileo’s observation, as made in Florence, March 1613.

1. G. Galilei, “Sidereus Nuncius” (”The Starry Messenger“) (1610) [↩]
2. G. Galilei, “Istoria e Dimostrazioni intorno alle Macchie Solari” (”The Sunspot Letters to Marc Welser”) (1613) [↩]
3. Massimo Mogi Vicentini, © Planetario di Milano, Italy [↩]

The genetic information of all living organisms is encoded into long sequences of four molecular symbols, structured like the steps of giant DNA ladders named chromosomes. Human cells contain two sets of 23 chromosomes, each having 50 to 250 millions symbols or base pairs for a total of 3 billions, like a book of one million pages written in a mostly unknown language. In this image, a short excerpt from human chromosome 20, which has 63 644 868 base pairs, is represented by using the letters A C G T and dots for apparently unused sections.

Click image to zoom¹

1. © Ben Fry, Computation Group MIT Media Lab [↩]

One of the most puzzling experiments in quantum physics is the quantum eraser, proposed by Scully and Drühl in 1982¹ and further implemented in several different settings.

A basic principle of quantum mechanics is complementarity, stating that for each degree of freedom, the dynamical variables are a pair of complementary observables. Being complementary means that precise knowledge of one implies complete unpredictability of the other. For example, precise knowledge of a particle position implies complete unpredictability of its momentum.

An illustration of complementarity is the classic double-slit experiment,² where monochromatic light going through a screen with two slits produces wave interference patterns. However, if a device is used to detect photons while they pass through each slit, the interference disappears. This non-classical dual behavior (which is not specific to photons, but common to any particles, atoms and molecules³) is observed even when a single particle at a time is sent to the slits, suggesting that it interferes with itself.⁴ Knowledge of the particle’s path is complementary to the appearance of a wave interference pattern, and according to the Englert-Greenberger duality relation, D²+V²≤1 (where D is the distinguishability of paths from 0 to 1 and V is the visibility of the interference pattern from 0 to 1).⁵

It has been considered that the general mechanism responsible for the loss of the interference pattern is the uncertainty principle, as no measure can be so delicate not to disturb the system which is measuring.⁶ However, in this experiment, the “which-way” information of the particles is found without disturbing their wavefunction. The reason of the interference loss is the quantum information contained in the measuring apparatus, by means of the entanglement correlations between the particles and the path detectors. The experiment shows that if such quantum information is afterwards erased from the system, then the interference reappears (which would be impossible in the case of a perturbation).

The original setting of the experiment involved beams of atoms,⁷ while further versions used light. ⁸ In the experiment presented here, by Kim et al.,⁹ photons from a laser beam pass through a double-slit and then hit a beta-barium borate crystal at point A or B depending on which slit they traversed. Such a crystal has a special optical property, namely when it absorbs a photon it re-emits from the same point a pair of entangled photons going in opposite directions (right and left in the figure below). This allows to determine the path of one photon by measuring the other, possibly even after the first already hit the detector, eg. by having one path shorter in length.

The photon going to the right is detected by D0, which is able to scan the x direction in order to eventually record an interference pattern. The photon going to the left is sent through a beam splitter (BSA or BSB depending on the initial path). A beam splitter is a semitransparent mirror, which has equal probability of reflecting or transmitting light. The photon exiting BSA may go to D3 or to a second beam splitter BS, and similarly the photon exiting BSB may go to D4 or to BS. Finally, photons exiting BS go to detectors D1 or D2.

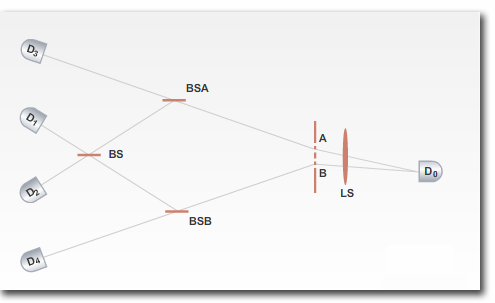
The left-side detectors record the which-way information:

• If D3 or D4 are hit, then it is known that the photons pair took respectively path A or B.

• If D1 or D2 are hit, then the path is no longer known (because D1 may be triggered both by a photon following path A through BSA-BS-D1, or by a photon following path B through BSB-BS-D1, the same happens for D2). The beam splitter BS is the eraser of the which-way information, mixing the two paths with equal probability.

The right-side detector records the interference pattern:

• When the right-side photon hits D0, the left-side photon is still in flight on a well-determined path. Accordingly, D0 does not show interference.

• The which-way information is then erased for all photons hitting D1 or D2, and not erased for all photons hitting D3 or D4.

At this point, it is possible to correlate the which-way information of these two groups of photons with the corresponding subset of photons detected at D0. We could paint eg in violet all hits at D0 corresponding to hits at D3 or D4, and we find that their distribution has no interference (according to the fact that the which-way information is known). We could then paint in red all hits at D0 corresponding to hits at D1, and in blue those corresponding to hits at D2, ie. after the erasure of the which-way information, and we find that their distribution shows two interference pattern, one with fringes for D1 and one with anti-fringes for D2, which cancel when added together.

At time T0 when D0 is triggered no interference appears, since the which-way information is contained in the system at that time. At time T1, which in the experiment is some nanoseconds later but could be in principle any time later,¹⁰ when D1/D2/D3/D4 are triggered, we find interference in the correlated subsets of past D0 records undergoing future erasure of the which-way information.

1. M. O. Scully, K. Drühl, “Quantum eraser - A proposed photon correlation experiment concerning observation and ‘delayed choice’ in quantum mechanics“, Phys. Rev. A, 25, 2208-2213 (1982) [↩]
2. T. Young, “Experimental Demonstration of the General Law of the Interference of Light”, Philosophical Transactions of the Royal Society of London, 94 (1804) [↩]
3. M. Arndt, O. Nairz, J. Vos-Andreae, C. Keller, G. van der Zouw, A. Zeilinger, “Wave-particle duality of C60 molecules“, Nature, 401, 680-682 (1999) [↩]
4. P. G. Merli, G. F. Missiroli, G. Pozzi, “On the statistical aspect of electron interference phenomena“, American Journal of Physics, 44, 3, 306-307 (1976) [↩]
5. B. G. Englert, “Fringe Visibility and Which-Way information: an inequality“, Phys. Rev. Lett. 77, 2154-2157 (1996) [↩]
6. N. Bohr, “Discussion with Einstein on Epistemological Problems in Atomic Physics”, in “Albert Einstein: Philosopher-Scientist”, ed. P. Schilpp, Tudor, New York (1949) [↩]
7. M. O. Scully, B. G. Englert, H. Walther, “Quantum optical tests of complementarity“, Nature, 351, 111-116 (1991) [↩]
8. S. P. Walborn, M. O. Terra Cunha, S. Pádua, C. H. Monken, “A double-slit quantum eraser“, Phys. Rev. A 65 (2002) [↩]
9. Y-H. Kim, R. Yu, S. P. Kulik, Y. H. Shih, M. O. Scully, “A Delayed Choice Quantum Eraser“, Phys. Rev. Lett. 84 1-5 (2000) [↩]
10. This “delayed-choice” is in the line of the thought experiment proposed by J. A. Wheeler in: “The ‘past’ and the ‘delayed-choice’ double-slit experiment”, “Mathematical Foundations of Quantum Theory”, Academic Press, New York (1978), see also V. Jacques, E. Wu, F. Grosshans, F. Treussart, P. Grangier, A. Aspect, J-F Roch, “Experimental realization of Wheeler’s delayed-choice GedankenExperiment“, arxiv:quant-ph/0610241 (2006) [↩]

Timelapse photo of the total lunar eclipse of October 27, 2004.¹ Celestial bodies orbiting around a star cast shadows, which may partially or totally obscure other bodies aligned behind them, “eclipsing” the star from their viewpoint (from Greek ekleipein, “failing to appear”).

Click image to zoom

Given their short duration, eclipses are amongst the phenomena where cosmic scale dynamics may be perceived most dramatically. In the picture, the moon’s curved path is primarily due to Earth’s rotation, and to a small extent to the lunar motion in its elliptical orbit around the Earth. During the totality stage the Moon appears red, because Earth’s atmosphere scatters sunlight and only red wavelengths are refracted into the shadow. An observer on the moon would see a bright ring of red light, coming from all simultaneous Earth’s sunrises and sunsets.²

A total lunar eclipse will happen Saturday, March 3, 2007, and will be visible from Europe, Africa, Western Asia and Eastern America.

1. Picture © Forrest J. Egan, Digital Astro [↩]
2. Eclipse seen from the moon, Surveyor 3 mission, 24 April 1967 (artificial color) © NASA [↩]

Caustics (from the Greek kaustikos, kaiein, ‘to burn’) are geometrical entities formed by the singular concentration of curves, which model approximately the behavior of light rays focused by lenses or curved mirrors, leading to very bright regions when they encounter a surface. The light patterns at the bottom of swimming pools are examples of caustics, produced by the refraction on the wavy surface of water. In this computer image are discovered light caustics produced by two consecutive wavy surfaces, as if light was entering a second sea under the sea.

Click image to zoom¹

1. Digital Artwork © Eric J. Heller, Resonance Fine Art [↩]

The concept of star travel, from planetary system to planetary system, is at the same time completely familiar and completely uncharted. Familiar, as we have certainly all heard of science fiction stories set on a far galaxy, where planets are nations or provinces of an empire. The characters usually move from one planet to another during intervals of time consistent with the story. The actual travel appears just like a formality, which the future advancements of a Triumphant Physics will put within reach.

This is what I’ll call the “strategy zero” (S0) : here travel is “instantaneous” or at the very least quicker than one year, eg. comparable to the durations of terrestrial travels or manned missions to the moon or other solar system’s bodies.

The way toward stars becomes however quite unfamiliar if we consider that such Triumph of Physics could possibly not happen, and that the famous constant of Einstein c, the speed of light (3E8 m/s), represents an horizon speed which is impossible to exceed and which is even extraordinarily difficult to approach, so that we would begin to see outer space like it is seen by astronomers: a vastness compared to which that of terrestrial oceans is nothing.

It is not without reserve that our mind adapts to the true dimensions of interstellar space. The insanity of these distances is not the only reason: in a sense, one could say that the “strategy zero” is enracined in a child’s desire of space. Not of a space-distance, of a horridly naked space, speechless and fearless, but of a space-treasure, and of the worlds which roll within its vastness. All these worlds whose reach should not suffer any delay and whose discovery turns on our imagination.
Realism helping, we leave with some regret the green paradise of “strategy zero”, but we can still consider a little more “teenager” strategy, within the framework of Special Relativity, which we will name “short strategy” or SI, which promises a travel duration within a man’s lifetime.

(More..)

Computer simulation of classical paths of electrons within a two-dimensional electron gas.¹ Transistors, the most common electronic devices, contain layered structures constraining the motion of electrons, so that they are free to move in the x-y plane but are completely confined in the z direction, forming a so-called two-dimensional electron gas (2DEG). The details of the electrons motion in a 2DEG flow were unknown until recently, when newly developed microscopy techniques made possible the observation of the actual electron paths. ²

Click image to zoom

Instead of a smooth flow, unexpected chaotic channeling was observed, with continuous branching of classical paths reminiscent of familiar natural forms. It has been found through simulation that these patterns are not due to preferred-energy paths in the background, like for the path of a river on a valley, but to the cumulative chaotic effect of encountering random positive “bumps” in the atomic landscape.

1. Digital Artwork © Eric J. Heller, Resonance Fine Art [↩]
2. M. A.Topinka, B. J. LeRoy, R. M. Westervelt, S. E. J. Shaw, R. Fleischmann, E. J. Heller, K. D. Maranowski, A. C. Gossard, “Coherent Branched Flow in a Two-Dimensional Electron Gas“, Nature, 410, 183 (2001) [↩]

Optical microscope photographs of snow crystals.¹ Their characteristic 6-fold symmetry is related to the molecular structure of water, which stabilizes in hexagonal lattices at earth temperature and pressure.² Each crystal has about 10¹⁸ molecules of water, and its very specific shape is due to a complex dependence on temperature and humidity change, and to nonlinear diffusion leading to structural branching instabilities and dendritic patterns. Each snowflake registers a history of interactions with the environment, like “a hyeroglyph sent from the sky”.³

Click image to zoom

1. © Kenneth G. Libbrecht (Caltech) [↩]
2. Water has several other possible solid phases, depending on pressure and temperature, with different crystal symmetry. Eg. ice-Ic forming at earth pressure and temperature lower than -80°C has cubic symmetry. [↩]
3. U. Nakaya, “Snow Crystals: Natural and Artificial”, Harvard University Press (1954) [↩]