Réaction aux propos de JP Luminet

Ache a écrit:

Je connais un fanatique qui voit en Leibniz le précurseur du XML (entre autres bien sûr). Donc on peut voir en Platon le précurseur des groupes de Lie - et l'inverse. Et pour continuer dans le fétichisme, Alain Connes s'exprime informellement sur la phrase du modèle standard, ici & là.

Excellente transition, voici le récent tour de force de Connes : une fonctionnelle d'action qui restitue l'intégralité du modèle standard couplé à la gravité de Einstein en termes de géométrie spectrale (Gilgamesh : c'est une bonne alternative si la formule de la page précédente ne rentre pas sur un T-shirt).

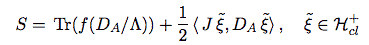
Code:

S=\,\Tr(f(D_A/\Lambda))+\frac
12\,\langle\,J\,\tilde\xi,D_A\,\tilde\xi\rangle\,,\quad\tilde\xi\in
\cH^+_{cl}

xantox a écrit:

Excellente transition, voici le récent tour de force de Connes : une fonctionnelle d'action qui restitue l'intégralité du modèle standard couplé à la gravité de Einstein en termes de géométrie spectrale (Gilgamesh : c'est une bonne alternative si la formule de la page précédente ne rentre pas sur un T-shirt).

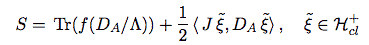
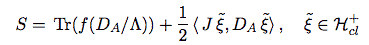
Code:

S=\,\Tr(f(D_A/\Lambda))+\frac
12\,\langle\,J\,\tilde\xi,D_A\,\tilde\xi\rangle\,,\quad\tilde\xi\in
\cH^+_{cl}

Mauvaise nouvelle pour les vendeurs de T-shirt (que je reposte illico dans le fil hardware ) .

Ce serait superbement sublime.

Tu sais ce que désignent les termes Da, Lambda, J, zêta, epsilon... ?

a+


edit : et S bien sûr (pour commencer)

Gilgamesh a écrit:

Tu sais ce que désignent les termes Da, Lambda, J, zêta, epsilon... ?

Le terme de gauche définit la partie bosonique et codifie l'action de Hilbert-Einstein. Celui de droite ajoute les fermions. La codification s'entend dans le cadre théorique de la géometrie spectrale :

S: fonctionnelle d'action spectrale
J: structure réelle sur le triplet spectral (A, H, D) associé au spectre du modèle standard (triplet qui codifie l'essentiel de l'information)
D_A: opérateur de Dirac
Λ: paramètre d'échelle d'énergie
ξ: spineur sur l'espace de Hilbert (variable de Grassmann)

waouh !!
Est-ce qu'on a le nouveau lagrangien (ou plutôt les termes en plus qu'Alain Connes a introduit, décrivant la gravitation ?) ?

bongo1981 a écrit:

waouh !!
Est-ce qu'on a le nouveau lagrangien (ou plutôt les termes en plus qu'Alain Connes a introduit, décrivant la gravitation ?) ?

Selut Bongo



Je serais bien en peine de te répondre mais j'en profite pour poster un lien vers un PDF sur la géométrie de la gravitation et du modèle standard, pour les courageux.

http://nivea.psycho.univ-paris5.fr/~phi ... ometry.pdf

a+

bongo1981 a écrit:

Est-ce qu'on a le nouveau lagrangien (ou plutôt les termes en plus qu'Alain Connes a introduit, décrivant la gravitation ?) ?

Pour la partie gravitationnelle on retrouve l'action de Hilbert-Einstein :



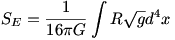
Aussi ce couplage avec la gravité (à basse énergie) n'est pas introduit spécifiquement, mais résulte intrinsèquement de la géometrie spectrale (cela prolonge les résultats passés de Connes généralisant toute métrique de Riemann par une géometrie spectrale associée à un opérateur de Dirac).

Les termes suivants de l'expansion restituent l'integralité du modèle standard, écrit en utilisant une métrique qui dépend du triplet spectral. En calculant la différentielle des équations de mouvement par rapport à la métrique on retrouve l'équation de Einstein.

Il faut ajouter qu'au délà du résultat mathématique en soi remarquable, la signification physique de cette réformulation n'est pas encore comprise.