Nous sommes le 21 Janvier 2026 00:05 UTC + 1 heure
Bonjour
Ce message fait suite aux commentaires postés à la suite de l'article principal.
Je vais donner ici les résultats de mes calculs concernant la répartition du carburant tout au long du trajet. Des réservoirs sont envoyés indépendament de l'arche, éventuellement avec leur propre système de propulsion. Je me suis limité au cas le plus économique où les réservoirs sont uniquement accélérés, jamais freinés..
Tout d'abord quelques calculs afin de confirmer l'intérêt de cette stratégie. Les calculs sont basés sur l'équation de Tsiolkovski.
Notations :
[tex]m[/tex] est la masse de la structure seule.
[tex]m_0[/tex] est la masse de carburant nécéssaire au voyage en une seule étape.
Lorsque le voyage est divisé en [tex]2n[/tex] étapes (il y a 2 phases : accélérération et freinage), donc avec l'envoi de [tex]2n-1[/tex] réservoirs indépendants, [tex]m_1[/tex] est la masse de carburant embarquée au départ de l'arche et [tex]m_i[/tex] pour [tex]i = 2...2n[/tex] sont les masses de carburant nécéssaires à la propulsion de chaque réservoir.
[tex]v[/tex] est la vitesse maximale de l'arche.
Pour simplifier, on suppose que le vitesse d'éjection des propulseur s est égale à 1, et que qu'un seul type de propulseur est utilisé, à la fois pour l'arche et ses réservoirs.
Pour chaque étape, la variation de vitesse de l'arche sera la même, à savoir [tex]\frac{v}{n}[\tex]. Par conséquent, d'après Tsiolkovski, chaque étape nécéssite la même quantité de carburant, que chaque réservoir devra transporter (sans consommer!). Cette quantité est celle consommée à la première étape : [tex]m_1[\tex]
Cas 1 : une seule étape (cas normal)
Tsiolkovski :
[tex]m_0 + m = m.e^{2v][/tex]
On a alors :
[tex]\frac{m_0}{m} = e^{2v} - 1[/tex]
((corrigé le 29/02 : merci à Gilgamesh qui a signalé l'erreur))
Cas 2 : un réservoir est envoyé à mi-chemin
Tsiolkovski :
[tex]m_1 + m = m.e^v[/tex]
[tex]m_2 + m_1 = m_1.e^v[\tex]
D'où :
[tex]m_1 = m . (e^v -1)[\tex]
[tex]m_1 + m_2 = m . (e^v-1) . e^v[\tex]
Finallement :
[tex]\frac{m_1+m_2}{m} = (e^v-1) . e^v[\tex]
Cas 3 : [tex]n=2[\tex] (3 réservoirs intermédiaires)
Je passe les détails...
[tex]m_1+m_2+m_3+m_4 = m . (e^v+e^\frac{3v}{2}-4e^\frac{v}{2}+2)[\tex]
Cas général :
C'est plus délicat...
Tsiolkovski :
[tex]m_1 + m = m.e^\frac{v}{n}[/tex]
Pour la phase d'accélération : i=2...n+1
[tex]m_i + m_1 = m_1.e^\frac{(i-1)v}{n}[\tex]
Pour pour la phase de freinage : i=n+2...2n
Comme la trajectoire est symétrique, considérons les étapes en commençant par la fin. Notons j = 2...n. On a alors :
[tex]j = 2n-i+2[\tex]
[tex]m_j + m_1 = m_1.e^\frac{(j-1)v}{n}[\tex]
Et donc :
[tex]m_i + m_1 = m_1.e^\frac{(2n-i+1)v}{n}[\tex]
D'où :
[tex]m_1 = m . (e^\frac{v}{n}-1)[\tex]
[tex]m_i = m . (e^\frac{v}{n}-1) . (e^\frac{(i-1)v}{n}-1)[\tex] pour i = 2 à n
[tex]m_{n+1} = m . (e^\frac{v}{n}-1) . (e^v-1)[\tex]
[tex]m_j = m . (e^\frac{v}{n}-1) . (e^\frac{(j-1)v}{n}-1)[\tex] pour j = 2 à n
Finallement :
[tex]\frac{\sum_{i=1}^{2n}m_i}{m} = (e^{\frac{v}{n}}-1) . [ 1 + \sum_{i=2}^{n}e^{\frac{(i-1)v}{n}} + (e^v - 1) + \sum_{j=2}^{n}e^{\frac{(j-1).v}{n}}][/tex]
On regroupe les sommes :
[tex]\frac{\sum_{i=1}^{2n}m_i}{m} = ( e^{\frac{v}{n}} - 1 ) [ 2 \sum_{i=2}^{n}e^{\frac{(i-1).v}{n}} -2(n-1) + e^v][/tex]
En changeant à nouveau d'indice :
[tex]\frac{\sum_{i=1}^{2n}m_i}{m} = ( e^{\frac{v}{n}} - 1 ) [ 2 \sum_{k=1}^{n-1}e^{\frac{kv}{n}} -2n+2 + e^v][/tex]
Oui je sais ça fait peur. En tout cas, à moi, ça m'a fait peur !
J'ai tant bien que mal glissé la formule dans mon tableur, et hop.
Interessant, non ? On verra que ce n'est pas si simple...
Xavier

economies.png [ 4.66 KB | Vu 145777 fois ]
Ce message fait suite aux commentaires postés à la suite de l'article principal.
Je vais donner ici les résultats de mes calculs concernant la répartition du carburant tout au long du trajet. Des réservoirs sont envoyés indépendament de l'arche, éventuellement avec leur propre système de propulsion. Je me suis limité au cas le plus économique où les réservoirs sont uniquement accélérés, jamais freinés..
Tout d'abord quelques calculs afin de confirmer l'intérêt de cette stratégie. Les calculs sont basés sur l'équation de Tsiolkovski.
Notations :
[tex]m[/tex] est la masse de la structure seule.
[tex]m_0[/tex] est la masse de carburant nécéssaire au voyage en une seule étape.
Lorsque le voyage est divisé en [tex]2n[/tex] étapes (il y a 2 phases : accélérération et freinage), donc avec l'envoi de [tex]2n-1[/tex] réservoirs indépendants, [tex]m_1[/tex] est la masse de carburant embarquée au départ de l'arche et [tex]m_i[/tex] pour [tex]i = 2...2n[/tex] sont les masses de carburant nécéssaires à la propulsion de chaque réservoir.
[tex]v[/tex] est la vitesse maximale de l'arche.
Pour simplifier, on suppose que le vitesse d'éjection des propulseur s est égale à 1, et que qu'un seul type de propulseur est utilisé, à la fois pour l'arche et ses réservoirs.
Pour chaque étape, la variation de vitesse de l'arche sera la même, à savoir [tex]\frac{v}{n}[\tex]. Par conséquent, d'après Tsiolkovski, chaque étape nécéssite la même quantité de carburant, que chaque réservoir devra transporter (sans consommer!). Cette quantité est celle consommée à la première étape : [tex]m_1[\tex]
Cas 1 : une seule étape (cas normal)
Tsiolkovski :
[tex]m_0 + m = m.e^{2v][/tex]
On a alors :
[tex]\frac{m_0}{m} = e^{2v} - 1[/tex]
((corrigé le 29/02 : merci à Gilgamesh qui a signalé l'erreur))
Cas 2 : un réservoir est envoyé à mi-chemin
Tsiolkovski :
[tex]m_1 + m = m.e^v[/tex]
[tex]m_2 + m_1 = m_1.e^v[\tex]
D'où :
[tex]m_1 = m . (e^v -1)[\tex]
[tex]m_1 + m_2 = m . (e^v-1) . e^v[\tex]
Finallement :
[tex]\frac{m_1+m_2}{m} = (e^v-1) . e^v[\tex]
Cas 3 : [tex]n=2[\tex] (3 réservoirs intermédiaires)
Je passe les détails...
[tex]m_1+m_2+m_3+m_4 = m . (e^v+e^\frac{3v}{2}-4e^\frac{v}{2}+2)[\tex]
Cas général :
C'est plus délicat...
Tsiolkovski :
[tex]m_1 + m = m.e^\frac{v}{n}[/tex]
Pour la phase d'accélération : i=2...n+1
[tex]m_i + m_1 = m_1.e^\frac{(i-1)v}{n}[\tex]
Pour pour la phase de freinage : i=n+2...2n
Comme la trajectoire est symétrique, considérons les étapes en commençant par la fin. Notons j = 2...n. On a alors :
[tex]j = 2n-i+2[\tex]
[tex]m_j + m_1 = m_1.e^\frac{(j-1)v}{n}[\tex]
Et donc :
[tex]m_i + m_1 = m_1.e^\frac{(2n-i+1)v}{n}[\tex]
D'où :
[tex]m_1 = m . (e^\frac{v}{n}-1)[\tex]
[tex]m_i = m . (e^\frac{v}{n}-1) . (e^\frac{(i-1)v}{n}-1)[\tex] pour i = 2 à n
[tex]m_{n+1} = m . (e^\frac{v}{n}-1) . (e^v-1)[\tex]
[tex]m_j = m . (e^\frac{v}{n}-1) . (e^\frac{(j-1)v}{n}-1)[\tex] pour j = 2 à n
Finallement :
[tex]\frac{\sum_{i=1}^{2n}m_i}{m} = (e^{\frac{v}{n}}-1) . [ 1 + \sum_{i=2}^{n}e^{\frac{(i-1)v}{n}} + (e^v - 1) + \sum_{j=2}^{n}e^{\frac{(j-1).v}{n}}][/tex]
On regroupe les sommes :
[tex]\frac{\sum_{i=1}^{2n}m_i}{m} = ( e^{\frac{v}{n}} - 1 ) [ 2 \sum_{i=2}^{n}e^{\frac{(i-1).v}{n}} -2(n-1) + e^v][/tex]
En changeant à nouveau d'indice :
[tex]\frac{\sum_{i=1}^{2n}m_i}{m} = ( e^{\frac{v}{n}} - 1 ) [ 2 \sum_{k=1}^{n-1}e^{\frac{kv}{n}} -2n+2 + e^v][/tex]
Oui je sais ça fait peur. En tout cas, à moi, ça m'a fait peur !
J'ai tant bien que mal glissé la formule dans mon tableur, et hop.
Interessant, non ? On verra que ce n'est pas si simple...
Xavier
Pièces jointes:
economies.png [ 4.66 KB | Vu 145777 fois ]
Dernière édition par xav71 le 28 Février 2008 10:44, édité 1 fois au total.
Oups, j'm'a planté. Je ne voulais pas ouvrir un nouveau sujet. 
C'est tout aussi bien d'ouvrir un fil pour cela, c'est plus simple à suivre.
Bel effort, mais la relecture, il me faut relever que :
1- Dans le cas normal (tout-en-un), la masse m0 de carburant nécessaire s'obtient par :
m0+m = m.e2v (et non ev)
Il faut en effet accélérer puis freiner, et on doit pour cela accélérer tout d'abord la masse nécessaire au freinage, ce qui se traduit par une mise au carré de l'exponentielle.
Pour v=0,3 (4500/15000), 2v=0,6
e0,3 = 1,35
e0,6 = 1,82
Soit 0,82 kg de carburant par kg de structure.
2- Dans le cas "2 étapes", si tu adoptes cette notation à la seconde étape (m2+m1=m1.ev au lieu de m2=m1.ev), la masse totale de carburant nécessaire à accélération et au freinage n'est pas m2+m1 mais bien m2+2m1, car le terme m1 du premier membre (accélération) ne note pas pas la même masse que le terme m1 du second membre (freinage), bien qu'il lui soit numériquement égale.
C'est d'ailleurs cette décomposition en deux étapes qui permet de bien comprendre pourquoi il faut mettre au carré l'exponentielle dans le cas tout en un, car cette décomposition permet de visualiser numériquement ce qui se passe à chaque étape: à l'accélération la masse Ma=(m1+m2) sert à accélérer Mb=(m1+m). Au freinage, il ne reste que Mb, et la masse m1 sert à freiner m. La masse totale de l'engin au départ est bien Ma+Mb=m2+2m1+m.
Après ces corrections, faudrait traiter à nouveau le cas par récurrence...
a+
 Gilgamesh a écrit:
Gilgamesh a écrit:1- Dans le cas normal (tout-en-un), la masse m0 de carburant nécessaire s'obtient par :
m0+m = m.e2v (et non ev)
m0+m = m.e2v (et non ev)
Oups. C'est une coquille (que je vais corriger). Mais comme ce résultat n'est pas utilisé par le suite, le graphique est juste : 0,82 x 25 = 20,5 Gt de carburant.
Je ne suis pas très à l'aise avec tex... qui ne marche plus, on dirait... Vais-je devoir refaire mon post ?
 Gilgamesh a écrit:
Gilgamesh a écrit:2- Dans le cas "2 étapes", si tu adoptes cette notation à la seconde étape (m2+m1=m1.ev au lieu de m2=m1.ev), la masse totale de carburant nécessaire à accélération et au freinage n'est pas m2+m1 mais bien m2+2m1, car le terme m1 du premier membre (accélération) ne note pas pas la même masse que le terme m1 du second membre (freinage), bien qu'il lui soit numériquement égale.
Je ne comprends pas. Je ne fais que reprendre la formule utilisée au début de l'article.
Je récapitule :
m1 est la masse de carburant embarquée par l'arche au départ. Ce carburant permet d'atteindre la vitesse v/n.
Puis pour i=2...2n :
mi est la masse de carburant nécessaire à chaque réservoir pour atteindre le point de rencontre i, soit à la vitesse (i-1).v/n dans la phase d'accélération, soit à la vitesse (2n-i+1).v/n dans la phase de freinage.
Chaque réservoir doit apporter à l'arche la quantité de carburant nécessaire pour atteindre le point de rencontre suivant, c'est-à-dire augmenter (ou diminuer) la vitesse de v/n. Donc chaque réservoir doit transporter une masse m1 de carburant pour l'arche (la même quantité est nécéssaire à chaque étape).
Ainsi, la masse initiale de chaque réservoir est mi + m1, et la masse finale au point de rencontre n'est plus que de m1. On néglige la structure et le système de propulsion.
L'équation de Tsiolkovski est donc :
mi + m1 = m1 . e(i-1).v/n
ou
mi + m1 = m1 . e(2n-i+1).v/n
Je crois comprendre ce qui te gène : dans le cas 1, j'utilise la formule intégrant l'accélération et le freinage (et j'avais oublié le coef), tandis que pour les cas suivants, j'utilise la formule ne concernant que l'un ou l'autre (pas de carré) car à chaque étape, l'arche est soit accélérée, soit freinée, mais pas les deux, tandis que les réservoirs sont toujours accélérés. D'ailleurs, la 1ère formule découle de la seconde.
A moins que je n'ai pas assez détaillé mon "modèle"...
Il y a 2n étapes. A chaque relais (entre 2 étapes) l'arche est alimentée par un réservoir : il y a par conséquent 2n-1 réservoirs. Une fois l'arche alimentée, le réservoir est abandoné. Ce n'est donc pas le même réservoir qui alimente l'arche pendant l'accélération et à l'étape symétrique (même vitesse) pendant le freinage (ce n'est pas possible sans freiner le réservoir). Chaque réservoir n'apporte donc à l'arche que le carburant nécéssaire pour une étape. Donc pas de carré ni autre complication.
En espérant avoir été plus clair. Je vais poster la "suite" de ma réflexion, avec des courbes qui j'espère permettront de mieux visualiser les trajectoires.
Xavier
Je dois m'absenter ce we, j'essaye de te répondre dimanche (ou lundi si je rentre tard).
a+
a+
Bonjour
Comme promis voici un peu plus de détails concernant ma suggestion.
J'ai renoncé à inonder le fil d'équations pas trop passionnantes. A la place voici un graphe que j'ai voulu aussi clair que possible. Pour les équations, vous pouvez consulter le script GNUplot (un fichier "texte") qui a permis la création du graphique.
Attention : les paramètres du graphique ne sont pas exactement ceux prévus pour l'arche. Les phases d'accélération et de freinage ont été allongées afin d'être visibles sur un graphique global. Ca ne change rien au principe. Pour obtenir le graphique exact, il suffit de modifier un paramètre dans le script et de le charger dans GNUplot.
Le graphe illustre le cas d'un voyage en 4 étapes, donc avec 3 réservoirs intermédiaires, à chacun étant associée une couleur.
Il y a beaucoup de courbes sur ce graphique. La trajectoire de l'arche est en rouge "épais". T est la durée du voyage, D est la distance jusqu'à Eridani Epsilon. Ta est la durée des phases d'accélération/freinage, Da est la distance parcourue pendant ces phases.
Les trajectoires des réservoirs sont encadrées par des rectangles vides : le coin inférieur gauche est le point de départ (t0), le coin supérieur droit est le point de rencontre avec l'arche (tau).
Les rectangles pleins (légèrement plus foncés) encadrent les phases d'accélération des réservoirs : le coin inférieur gauche est toujours le point de départ, le coin supérieur droit indique le début du vol libre (theta) (ou la rencontre avec l'arche).
Une ligne droite oblique est associée à chaque réservoir. Cette droite est tangente à la fois à la trajectoire de l'arche (au point de rencontre prévu) et la celle du réservoir correspondant. La pente de cette droite représente la vitesse de l'arche au point de rencontre, et donc la vitesse que doit atteindre le réservoir (avant le point de rencontre!). Le réservoir accélère jusqu'à atteindre tangentiellement cette droite, qui représente ensuite la trajectoire du réservoir en vol libre jusqu'au point de rencontre.
Au dessus de cette droite, une zone est colorée jusqu'à une autre courbe (couleur claire). Cette parabole représente la trajectoire extrême du réservoir correspondant, celle où le réservoir atteint la tangente au dernier moment (le point de rencontre). Toutes les trajectoires possibles du réservoir sont incluses dans la zone colorée.
Remarques :
Les trajectoires extrêmes pour les réservoirs 1 et 2 sont peu visibles car confondues avec la trajectoire de l'arche.
La zone colorée du réservoir 1 est recouverte par celle du réservoir 2. Si vous touvez une solution...
Ces équations sont relativement simples. Je les ai obtenues par la résolution de 2 petit systèmes linéaires : un quand la rencontre doit avoir lieu pendant la phase d'accélération de l'arche (réservoirs 1 et 2) et un pendant la phase de freinage (réservoir 3).
Les systèmes sont de la forme :
D'une part :
A(tau) = T(tau) et dA/dt (tau) = dT/dt (tau)
Ce qui me donne T(t)
Et d'autre part :
R(theta) = T(theta) et dR/dt (theta) = dT/dt (theta)
A est la trajectoire de l'arche, R est la trajectoire du réservoir en accélération, et T est la tangente commune.
tau est la date de la rencontre et theta est la date de fin d'accélération du réservoir.
La trajectoire du réservoir dépend également de la date de départ du réservoir t0 et de l'accélération du réservoir aR. Sur le graphique j'ai choisi de fixer tau (évidement) et aR (2 fois l'accélération de l'arche). En modifiant légèrement le script (le cas est prévu) on peut fixer t0 et tau.
Ces systèmes ne sont pas vraiment complexes (tout est linéaire/rationnel). Mais la résolution est compliquée par le nombre de paramètres. Il faut donc être très attentif, ou alors, comme moi, perdre beaucoup de temps
J'espère cette fois-ci avoir été assez clair. N'hésitez pas à utiliser GNUplot pour visualiser différents cas ou aggrandir des zones, c'est pas si compliqué : il suffit d'un éditeur de texte.
Xavier
Comme promis voici un peu plus de détails concernant ma suggestion.
J'ai renoncé à inonder le fil d'équations pas trop passionnantes. A la place voici un graphe que j'ai voulu aussi clair que possible. Pour les équations, vous pouvez consulter le script GNUplot (un fichier "texte") qui a permis la création du graphique.
Attention : les paramètres du graphique ne sont pas exactement ceux prévus pour l'arche. Les phases d'accélération et de freinage ont été allongées afin d'être visibles sur un graphique global. Ca ne change rien au principe. Pour obtenir le graphique exact, il suffit de modifier un paramètre dans le script et de le charger dans GNUplot.
Le graphe illustre le cas d'un voyage en 4 étapes, donc avec 3 réservoirs intermédiaires, à chacun étant associée une couleur.
Il y a beaucoup de courbes sur ce graphique. La trajectoire de l'arche est en rouge "épais". T est la durée du voyage, D est la distance jusqu'à Eridani Epsilon. Ta est la durée des phases d'accélération/freinage, Da est la distance parcourue pendant ces phases.
Les trajectoires des réservoirs sont encadrées par des rectangles vides : le coin inférieur gauche est le point de départ (t0), le coin supérieur droit est le point de rencontre avec l'arche (tau).
Les rectangles pleins (légèrement plus foncés) encadrent les phases d'accélération des réservoirs : le coin inférieur gauche est toujours le point de départ, le coin supérieur droit indique le début du vol libre (theta) (ou la rencontre avec l'arche).
Une ligne droite oblique est associée à chaque réservoir. Cette droite est tangente à la fois à la trajectoire de l'arche (au point de rencontre prévu) et la celle du réservoir correspondant. La pente de cette droite représente la vitesse de l'arche au point de rencontre, et donc la vitesse que doit atteindre le réservoir (avant le point de rencontre!). Le réservoir accélère jusqu'à atteindre tangentiellement cette droite, qui représente ensuite la trajectoire du réservoir en vol libre jusqu'au point de rencontre.
Au dessus de cette droite, une zone est colorée jusqu'à une autre courbe (couleur claire). Cette parabole représente la trajectoire extrême du réservoir correspondant, celle où le réservoir atteint la tangente au dernier moment (le point de rencontre). Toutes les trajectoires possibles du réservoir sont incluses dans la zone colorée.
Remarques :
Les trajectoires extrêmes pour les réservoirs 1 et 2 sont peu visibles car confondues avec la trajectoire de l'arche.
La zone colorée du réservoir 1 est recouverte par celle du réservoir 2. Si vous touvez une solution...
Ces équations sont relativement simples. Je les ai obtenues par la résolution de 2 petit systèmes linéaires : un quand la rencontre doit avoir lieu pendant la phase d'accélération de l'arche (réservoirs 1 et 2) et un pendant la phase de freinage (réservoir 3).
Les systèmes sont de la forme :
D'une part :
A(tau) = T(tau) et dA/dt (tau) = dT/dt (tau)
Ce qui me donne T(t)
Et d'autre part :
R(theta) = T(theta) et dR/dt (theta) = dT/dt (theta)
A est la trajectoire de l'arche, R est la trajectoire du réservoir en accélération, et T est la tangente commune.
tau est la date de la rencontre et theta est la date de fin d'accélération du réservoir.
La trajectoire du réservoir dépend également de la date de départ du réservoir t0 et de l'accélération du réservoir aR. Sur le graphique j'ai choisi de fixer tau (évidement) et aR (2 fois l'accélération de l'arche). En modifiant légèrement le script (le cas est prévu) on peut fixer t0 et tau.
Ces systèmes ne sont pas vraiment complexes (tout est linéaire/rationnel). Mais la résolution est compliquée par le nombre de paramètres. Il faut donc être très attentif, ou alors, comme moi, perdre beaucoup de temps
J'espère cette fois-ci avoir été assez clair. N'hésitez pas à utiliser GNUplot pour visualiser différents cas ou aggrandir des zones, c'est pas si compliqué : il suffit d'un éditeur de texte.
Xavier
Pièces jointes:
Commentaire: Trajectoires de l'arche et de 3 réservoirs

arche.png [ 9.14 KB | Vu 146253 fois ]
arche.png [ 9.14 KB | Vu 146253 fois ]
Superbe travail xav 
 et tu me fait en outre découvrir GnuPlot qui me semble assez impressionnant.
et tu me fait en outre découvrir GnuPlot qui me semble assez impressionnant.
J'ai téléchargé le soft et ton .plt et ça marche nickel.
J'aimerais bien essayer de calculer la trajectoire avec une poussée fixe - donc une accélération croissante - qui représente un cas plus réaliste dans la mesure où les moteurs sont à puissance maximale dès le départ, tu pourrais me cornaquer un peu au niveau de la syntaxe des calculs ?
merci encore.
a+
J'ai téléchargé le soft et ton .plt et ça marche nickel.
J'aimerais bien essayer de calculer la trajectoire avec une poussée fixe - donc une accélération croissante - qui représente un cas plus réaliste dans la mesure où les moteurs sont à puissance maximale dès le départ, tu pourrais me cornaquer un peu au niveau de la syntaxe des calculs ?
merci encore.
a+
Citer:
Superbe travail xav 
 et tu me fait en outre découvrir GnuPlot qui me semble assez impressionnant.
et tu me fait en outre découvrir GnuPlot qui me semble assez impressionnant.
J'ai téléchargé le soft et ton .plt et ça marche nickel.
J'ai téléchargé le soft et ton .plt et ça marche nickel.
Merci
Citer:
J'aimerais bien essayer de calculer la trajectoire avec une poussée fixe - donc une accélération croissante - qui représente un cas plus réaliste dans la mesure où les moteurs sont à puissance maximale dès le départ
Oula, ça doit pas mal compliquer les calculs, ça... L'accélération évolurait comment ? Va falloir sortir les équa-diff
Citer:
tu pourrais me cornaquer un peu au niveau de la syntaxe des calculs ?
Te sens-tu une âme de pachyderme ?
Je ne suis pas un spécialiste de GNUplot, mais je peux essayer d'identifier quelques pièges dans lesquels je suis tombé.
Je précise d'abord que GNUplot est bête : c'est pas lui qui va ressoudre la moindre équation. Ca me fait penser qu'il va falloir que je m'essaie à un logiciel comme Maxima.
Prenons l'exemple du script plus haut. Il y a (en gros) deux parties : la définition des valeurs et des fonctions, et le tracé lui-même. La séparation est facultative : c'est un choix personnel pour essayer d'avoir un script un peu plus clair.
A mon avis, la partie définition ne pose pas particulièrement de problème : c'est très intuitif. Une petite difficuté peut-être : l'opérateur conditionnel, qui peut surprendre si on ne connait pas le language C.
Code:
(condition)? (si oui) : (si non)
Les parenthèses sont facultatives, mais conseillées pour éviter les problèmes d'ordre d'évaluation des opérateurs.
Exemple :
Code:
abs(x) = (x>0)? x : -x
(je suppose que cette fonction existe déjà...)
J'ai utilisé "?:" dans deux cas :
1) pour définir des fonctions par intervalles (comme la valeur absoue)
2) pour limiter le tracé à un intervalle donné : en dehors de l'intervalle je retourne la valeur 1/0 qui est une erreur et ne trace rien.
Un autre point qui peu géner la lecture : le signe "\" indique que la commande en cours continue sur la ligne suivante. Ca permet d'introduire une mise en page simplifiée:
Code:
abs(x) = (x>0) ? x \
: -x
: -x
Ou encore (dans le script plus haut) :
Code:
t0(aR,tau) = (tau<T-Ta)? ( \
0.5*tau*(1-a/aR) \
):( \
0.5*(2*D/a/(tau-T)+tau+T + a/aR*(tau-T)) \
)
0.5*tau*(1-a/aR) \
):( \
0.5*(2*D/a/(tau-T)+tau+T + a/aR*(tau-T)) \
)
est exactement équivalent à :
Code:
t0(aR,tau) = (tau<T-Ta)? ( 0.5*tau*(1-a/aR) ):( 0.5*(2*D/a/(tau-T)+tau+T + a/aR*(tau-T)) )
Pour la seconde partie, c'est plus délicat car les paramètres sont très nombreux. Il y a plusieurs "étapes" pour définir un tracé. Tout d'abord il faut définir les objets qui ne sont pas des courbes : les axes, la legende, des étiquettes, des flêches, des rectangles... Les définitions de ces objets sont mémorisées, et ils sont affichés chaque fois que la commande "plot" est utilisée.
La commande "plot" permet de tracer une courbe, soit d'après une fonction, soit d'après des données numériques stockées dans un fichier. Normalement, chaque "plot" commence un nouveau graphique, mais il est possible d'utiliser plusieur fois le même graphique avec la commande "set multiplot" : les tracés se superposent alors, l'ordre peut donc être important. Attention : chaque "plot" trace ses propres axes, sa propre échelle, sa propre légende, etc... Il faut donc qu'ils soient identiques, ou désactivés, ou encore que la mise en page soit adaptée.
Un dernier point : le tracé se fait sur un certain type de "terminal". Chaque type de terminal a ses propres fonctionnalités et limitations. Par conséquent le résultat pourra être différent selon le terminal choisi. Ainsi, pour le graphique plus haut j'ai préféré faire une copie d'écran sous windows plutôt que d'écrire directement dans un fichier png, qui aurait été moins complet.
Le fichier d'aide qui accompagne le logiciel n'est pas très bien fait, mais il y a de nombreux sites web qui donnent des actuces, y compris en français, accessibles à partir du site officiel.
Si tu as des soucis, n'hésite pas à me demander, y compris par courrier. On sait jamais, j'aurais peut-être déjà rencontré le problème.
Xavier
Ayé, j'y suis arrivé.
Pour une arche de masse initiale m, éjectant un débit massique q à la vitesse u,
L'expression de l'accélération a en fonction du temps t est :
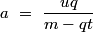
La vitesse v est :
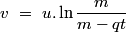
L'abscisse x est :
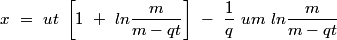
Code LaTeX :
a\ =\ \frac{uq}{m-qt}
v\ =\ u.\ln\frac{m}{m-qt}
x\ =\ ut\ \left[1\ +\ ln\frac{m}{m-qt}\right]\ -\ \frac{1}{q}\ um\ ln\frac{m}{m-qt}
Pour une arche de masse initiale m, éjectant un débit massique q à la vitesse u,
L'expression de l'accélération a en fonction du temps t est :
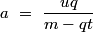
La vitesse v est :
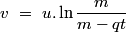
L'abscisse x est :
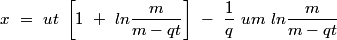
Code LaTeX :
Code:
a\ =\ \frac{uq}{m-qt}
v\ =\ u.\ln\frac{m}{m-qt}
x\ =\ ut\ \left[1\ +\ ln\frac{m}{m-qt}\right]\ -\ \frac{1}{q}\ um\ ln\frac{m}{m-qt}
  |
Page 1 sur 1 |
[ 9 messages ] |
|
Qui est en ligne |
Utilisateurs parcourants ce forum : Aucun utilisateur inscrit et 30 invités |
| Vous ne pouvez pas publier de sujets Vous ne pouvez pas répondre aux sujets Vous ne pouvez pas éditer vos messages Vous ne pouvez pas supprimer vos messages Vous ne pouvez pas insérer des pièces jointes |
