Nous sommes le 08 Octobre 2025 15:48 UTC + 1 heure
Un petit fil pour présenter la traduction d'un paragraphe d'un ouvrage d'André Linde [également cité dans Ressources > Livres et cours en lignes > Cosmologie] et publié in extenso sur arxiv.
Le paragraphe concerne l'espace de De Sitter, ses caractéristiques, ses bizarreries, et le lien profond qui existe avec les espaces inflationnaires.
On se souviendra que l'espace de De Sitter est, dans l'histoire de la cosmologie, une des première solution, statique, des équations d'Einstein appliquées à l'Univers. Par l'effet d'une ironie charmante, la phase inflationnaire qui présente des analogies profondes avec lui représente la phase explosive de croissance du jeune l'Univers, au cours de laquelle il va manifester, comme jamais par la suite, son caractère dynamique.
PARTICLE PHYSICS
AND INFLATIONARY COSMOLOGY
Andrei Linde
Department of Physics, Stanford University, Stanford CA 94305-4060, USA
LaTeX version of my book “Particle Physics and Inflationary Cosmology” (Harwood, Chur, Switzerland, 1990). "Particle Physics and Inflationary Cosmology", Harwood (1990), repr. in Contemp. Concepts Phys. 5, 1-362 (2005) (arXiv hep-th/0503203).
7.2 L'univers inflationnaire et l'espace de De Sitter
Comme nous l'avons déja noté au Chap. 1 la principale caractéristique de l'étape inflationnaire est la lente variation (lente comparée avec le taux d'expansion) de la densité d'énergie ρ. Dans le cas limité à ρ=cte l'équation d'Einstein pour un univers homogène a l'espace de de Sitter comme solution.
Il est facile de voir que quand Ht >> 1, la distinction entre un espace de Sitter ouvert, fermé et plat tend à disparaître. Ce qui est moins évident, c'est le fait que ces trois solutions décrivent en réalité exactement le même espace de de Sitter.
Pour aider à l'interprétation intuitive d'un espace 4D courbé, il est souvent pratique de l'imaginer plongé dans un espace de dimension supérieur. La façon la plus simple de représenter l'espace de Sitter est l'hyperboloïde :
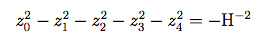
dans l'espace de Minkowski à 5 dimension (z0, z1, ..., z4). Pour représenter l'espace de Sitter comme un univers de Friedmann plat il suffit de considérer un système de coordonnée t, xi sur l'hyperboloïde défini par les relations :
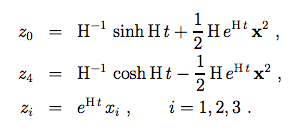
Ce système de coordonnées couvre la moitié de l'hyperboloïde avec z0 + z4 > 0 et sa métrique prend la forme :
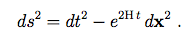 (7.2.3)
(7.2.3)
L'espace de de Sitter ressemble à un univers Friedmann fermé, dans le système de coordonnées (t, χ, θ, φ) défini par :
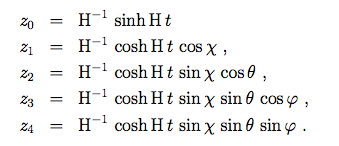
La métrique devient alors :
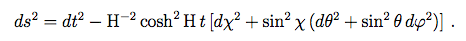 (7.2.5)
(7.2.5)
Il est important de noter que par contraste avec la métrique de l'univers plat et de celle d'un espace de Sitter ouvert (que nous ne détaillerons pas ici), la métrique de l'univers clot décrit la totalité de l'hyperboloïde. Dans la terminologie de la RG, on peut dire que l'espace de Sitter clot, à la différence de celui ouvert ou plat, est géodésiquement complet.
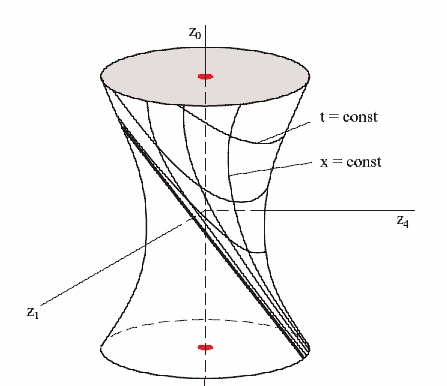
Pour aider à la compréhension de ce que cela signifie, il est utile ici de dresser une analogie avec ce qui se passe près d'un trou noir. En particulier, la métrique de Schwarzschild ne donne une description des événement près du rayon gravitationnel rg du trou noir, mais il existe un système de coordonnées qui permet de décrire ce qui se passe à l'intérieur du trou noir. Dans le cas présent, l'analogue de la métrique de Schwarzschild est la métrique de l'espace de Sitter plat (ou ouvert). Une analogie encore plus complete est donnée par les coordonnées statiques (r, t, θ, φ) :
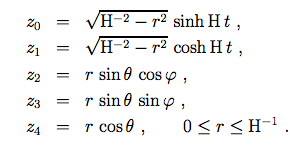
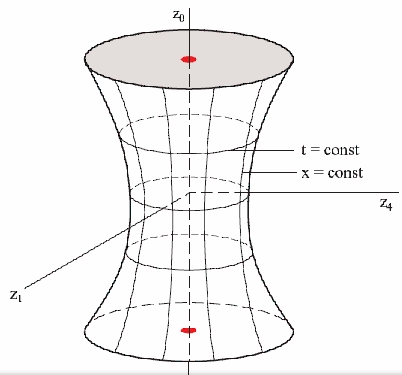
Ces coordonnées couvrent la partie de l'espace de Sitter avec z0 +z1 > 0, et la métrique prend la forme:
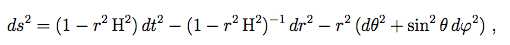 (7.2.7)
(7.2.7)
ressemblant à la forme de la métrique de Schwarzschild :
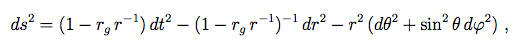 ( 7.2.8 )
( 7.2.8 )
où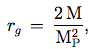 avec M la masse du trou noir. Ces deux équations démontrent que l'espace de Sitter en coordonnées statiques comprend une région de rayon H-1 qui est comme si elle était entourée par un trou noir. Ce résultat est relié à l'interprétation physique au Chap. 1, par l'introduction du concept d'horizon des événements. L'analogie entre les propriétés de l'espace de Sitter et celles d'un trou noir est très importante pour la compréhension de beaucoup d'aspects du scénario inflationnaire, et mérite par conséquent une discussion plus approfondie.
avec M la masse du trou noir. Ces deux équations démontrent que l'espace de Sitter en coordonnées statiques comprend une région de rayon H-1 qui est comme si elle était entourée par un trou noir. Ce résultat est relié à l'interprétation physique au Chap. 1, par l'introduction du concept d'horizon des événements. L'analogie entre les propriétés de l'espace de Sitter et celles d'un trou noir est très importante pour la compréhension de beaucoup d'aspects du scénario inflationnaire, et mérite par conséquent une discussion plus approfondie.
Il est bien connu que toutes perturbations d'un trou noir sont rapidement amorties et que les seules caractéristiques observables qui restent sont sa masse (ainsi que sa charge électrique et son moment angulaire s'il est en rotation). Aucune information sur les processus physiques se déroulant à l'intérieur ne quitte sa surface (c'est à dire l'horizon situé à r =rg). Cet état de fait est bien connu dans la littérature sous la forme d'un théorème qui énonce que "les trous noirs n'ont pas de cheveux".
La généralisation de ce "théorème" à l'espace de Sitter se traduit par le fait que toute perturbation dans le passé va être "oubliée" à un taux exponentiel, c'est à dire après un temps t >> H-1, l'univers devient localement indiscernable d'un espace de Sitter totalement homogène et isotrope. D'un autre côté, a cause de l'existence d'un horizon des événements, tous les processus physiques au sein d'une région donnée de l'espace de Sitter sont indépendants par rapport à n'importe quel autre situé à une distance plus grande que H-1.
La signification physique de la première partie du théorème est particulèrement claire dans le système de coordonnée (7.2.3) (ou (7.2.5) quand t >>H-1) : toute perturbation de l'espace de Sitter entrainé par l'expansion cosmologique va être exponentiellement étirée. Par conséquent, les gradients spatiaux de la métrique, qui caractérisent l'inhomogénéité locale et l'anisotropie de l'univers, vont être exponentiellement aplatis. Cette situation, qui a été vérifiée pour une large classe de modèles spécifiques, forme la base d'une solution à au problème de l'homogénéité et le l'isotropie dans l'univers inflationnaire.
La signification de la deuxième partie du théorème est que si la taille initiale d'une région inflationnaire excède la distance de l'horizon (r > H-1), alors aucun événement extérieur à cette région ne peut entraver cette inflation, vu qu'aucune information concernant ces événements ne peut jamais l'atteindre. On peut considérer l'indifférences des régions inflationnaires pour ce qui se passe à côté comme une sorte d'égoïsme inoffensif : la croissance de la région inflationnaire dépend uniquement de ses vertus propre et non de celles du voisinage. Ce type de processus (inflation chaotique) conduit finalement à un univers de structure très complexe à des échelles énormes mais à l'intérieur de chaque région inflationnaire l'univers semble localement uniforme à un haut dégré.
Cet élément joue un rôle important dans toute discussion concernant les conditions initiales requises pour initier un processus inflationnaire ou pour rechercher la structure globale de l'univers.
[..] Autre remarque au sujet du rapport entre un univers de Sitter et un univers inflationnaire : beaucoup d'ouvrages sur la RG disent que l'espace de Sitter n'est qu'un espace statique. Comme nous l'avons montré précédemment, pourtant, l'espace décrit par la métrique ( 7.2.7 ) est géodésiquement incomplet, c'est à dire qu'il existe des géodésiques qui conduisent hors de l'espace ( 7.2.7 ). De la même façon, un observateur qui tombe dans un trou noir ne note rien d'exceptionnel durant son plongeon final à travers la sphère de Schwarzschild r = rg, ainsi dans un espace de Sitter quelqu'un situé au point initial r = r0 < H-1 émerge de cette région décrite par les coordonnées ( 7.2.7 ) après un temps propre fini. (Tandis que cela a lieu, un observateur stationnaire situé à r = ∞ dans une métrique ( 7.2.8 ) ou à t = 0 dans la métrique (7.2.7) ne doit pas s'attendre à voir son ami disparaître derrière l'horizon, mais il recevra de lui de moins en moins d'information. [..]
En l'absence d'observateurs, de matière, ou encore de particules de test, ce défaut de stationnarité est "sui generis" vu que les caractéristiques invariantes de l'espace de Sitter associé au tenseur de courbure sont indépendantes du temps. Ainsi, par exemple, la courbure scalaire de l'espace de Sitter est:
R = 12H2 = cte
Par conséquent, si l'univers inflationnaire était simplement un espace de Sitter vide, il serait difficile de parler de son expansion. Il sera toujours possible de trouver un système de coordonnées dans lequel l'espace de Sitter semble, par exemple, comme s'il était en contraction, ou comme s'il avait une taille H-1 (équations (7.2.5) et (7.2.7)).
Mais dans l'univers inflationnaire, l'invariance de de Sitter est ou bien brisée spontanément (du fait de la décroissance du vide de Sitter initial) ou bien brisée du fait d'une disparité initiale entre l'univers actuel et l'espace de Sitter. En particulier, le tenseur énergie-impulsion Tμν dans le scénario d'inflation chaotique, bien qu'il soit proche de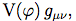 ne lui est jamais exactement égal, et dans les dernières étapes de l'inflation, l'ordre de grandeur du champs d'énergie cinétique
ne lui est jamais exactement égal, et dans les dernières étapes de l'inflation, l'ordre de grandeur du champs d'énergie cinétique
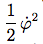
devient grand comparé à V(φ), et la différence entre Tμν et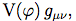 devient significative.
devient significative.
La distinction entre un espace statique de Sitter et l'univers inflationnaire devient spécialement claire au niveau quantique, quand on analyse les inhomogénéités de densité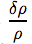 qui surviennent durant le temps de l'inflation.
qui surviennent durant le temps de l'inflation.
Comme nous le montrerons dans la Sect. 7.5, à la fin de l'inflation, ces inhomogénéités croissent de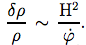
Ainsi, si le champs φ était constant et que l'univers inflationnaire ne pouvait être distingué d'un espace de Sitter, alors après l'inflation notre univers serait hautement inhomogène. En d'autres termes, un traitement correct de l'univers inflationnaire requiert que l'on ne prenne pas seulement en compte ses similitudes avec un espace de Sitter mais également ses différences, spécialement dans les derniers stades de l'inflation, quand la structure de la partie observable de l'univers fut formée.
Le paragraphe concerne l'espace de De Sitter, ses caractéristiques, ses bizarreries, et le lien profond qui existe avec les espaces inflationnaires.
On se souviendra que l'espace de De Sitter est, dans l'histoire de la cosmologie, une des première solution, statique, des équations d'Einstein appliquées à l'Univers. Par l'effet d'une ironie charmante, la phase inflationnaire qui présente des analogies profondes avec lui représente la phase explosive de croissance du jeune l'Univers, au cours de laquelle il va manifester, comme jamais par la suite, son caractère dynamique.
PARTICLE PHYSICS
AND INFLATIONARY COSMOLOGY
Andrei Linde
Department of Physics, Stanford University, Stanford CA 94305-4060, USA
LaTeX version of my book “Particle Physics and Inflationary Cosmology” (Harwood, Chur, Switzerland, 1990). "Particle Physics and Inflationary Cosmology", Harwood (1990), repr. in Contemp. Concepts Phys. 5, 1-362 (2005) (arXiv hep-th/0503203).
7.2 L'univers inflationnaire et l'espace de De Sitter
Comme nous l'avons déja noté au Chap. 1 la principale caractéristique de l'étape inflationnaire est la lente variation (lente comparée avec le taux d'expansion) de la densité d'énergie ρ. Dans le cas limité à ρ=cte l'équation d'Einstein pour un univers homogène a l'espace de de Sitter comme solution.
Il est facile de voir que quand Ht >> 1, la distinction entre un espace de Sitter ouvert, fermé et plat tend à disparaître. Ce qui est moins évident, c'est le fait que ces trois solutions décrivent en réalité exactement le même espace de de Sitter.
Pour aider à l'interprétation intuitive d'un espace 4D courbé, il est souvent pratique de l'imaginer plongé dans un espace de dimension supérieur. La façon la plus simple de représenter l'espace de Sitter est l'hyperboloïde :
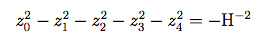
dans l'espace de Minkowski à 5 dimension (z0, z1, ..., z4). Pour représenter l'espace de Sitter comme un univers de Friedmann plat il suffit de considérer un système de coordonnée t, xi sur l'hyperboloïde défini par les relations :
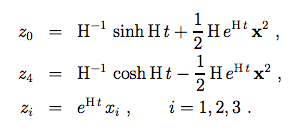
Ce système de coordonnées couvre la moitié de l'hyperboloïde avec z0 + z4 > 0 et sa métrique prend la forme :
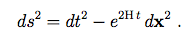 (7.2.3)
(7.2.3)L'espace de de Sitter ressemble à un univers Friedmann fermé, dans le système de coordonnées (t, χ, θ, φ) défini par :
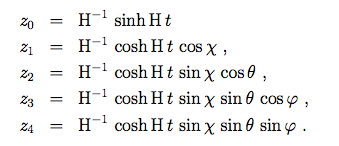
La métrique devient alors :
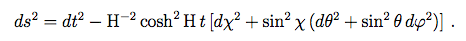 (7.2.5)
(7.2.5)Il est important de noter que par contraste avec la métrique de l'univers plat et de celle d'un espace de Sitter ouvert (que nous ne détaillerons pas ici), la métrique de l'univers clot décrit la totalité de l'hyperboloïde. Dans la terminologie de la RG, on peut dire que l'espace de Sitter clot, à la différence de celui ouvert ou plat, est géodésiquement complet.

Pour aider à la compréhension de ce que cela signifie, il est utile ici de dresser une analogie avec ce qui se passe près d'un trou noir. En particulier, la métrique de Schwarzschild ne donne une description des événement près du rayon gravitationnel rg du trou noir, mais il existe un système de coordonnées qui permet de décrire ce qui se passe à l'intérieur du trou noir. Dans le cas présent, l'analogue de la métrique de Schwarzschild est la métrique de l'espace de Sitter plat (ou ouvert). Une analogie encore plus complete est donnée par les coordonnées statiques (r, t, θ, φ) :
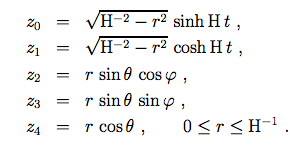

Ces coordonnées couvrent la partie de l'espace de Sitter avec z0 +z1 > 0, et la métrique prend la forme:
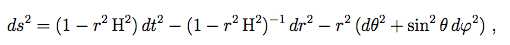 (7.2.7)
(7.2.7)ressemblant à la forme de la métrique de Schwarzschild :
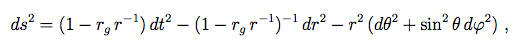 ( 7.2.8 )
( 7.2.8 )où
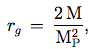 avec M la masse du trou noir. Ces deux équations démontrent que l'espace de Sitter en coordonnées statiques comprend une région de rayon H-1 qui est comme si elle était entourée par un trou noir. Ce résultat est relié à l'interprétation physique au Chap. 1, par l'introduction du concept d'horizon des événements. L'analogie entre les propriétés de l'espace de Sitter et celles d'un trou noir est très importante pour la compréhension de beaucoup d'aspects du scénario inflationnaire, et mérite par conséquent une discussion plus approfondie.
avec M la masse du trou noir. Ces deux équations démontrent que l'espace de Sitter en coordonnées statiques comprend une région de rayon H-1 qui est comme si elle était entourée par un trou noir. Ce résultat est relié à l'interprétation physique au Chap. 1, par l'introduction du concept d'horizon des événements. L'analogie entre les propriétés de l'espace de Sitter et celles d'un trou noir est très importante pour la compréhension de beaucoup d'aspects du scénario inflationnaire, et mérite par conséquent une discussion plus approfondie. Il est bien connu que toutes perturbations d'un trou noir sont rapidement amorties et que les seules caractéristiques observables qui restent sont sa masse (ainsi que sa charge électrique et son moment angulaire s'il est en rotation). Aucune information sur les processus physiques se déroulant à l'intérieur ne quitte sa surface (c'est à dire l'horizon situé à r =rg). Cet état de fait est bien connu dans la littérature sous la forme d'un théorème qui énonce que "les trous noirs n'ont pas de cheveux".
La généralisation de ce "théorème" à l'espace de Sitter se traduit par le fait que toute perturbation dans le passé va être "oubliée" à un taux exponentiel, c'est à dire après un temps t >> H-1, l'univers devient localement indiscernable d'un espace de Sitter totalement homogène et isotrope. D'un autre côté, a cause de l'existence d'un horizon des événements, tous les processus physiques au sein d'une région donnée de l'espace de Sitter sont indépendants par rapport à n'importe quel autre situé à une distance plus grande que H-1.
La signification physique de la première partie du théorème est particulèrement claire dans le système de coordonnée (7.2.3) (ou (7.2.5) quand t >>H-1) : toute perturbation de l'espace de Sitter entrainé par l'expansion cosmologique va être exponentiellement étirée. Par conséquent, les gradients spatiaux de la métrique, qui caractérisent l'inhomogénéité locale et l'anisotropie de l'univers, vont être exponentiellement aplatis. Cette situation, qui a été vérifiée pour une large classe de modèles spécifiques, forme la base d'une solution à au problème de l'homogénéité et le l'isotropie dans l'univers inflationnaire.
La signification de la deuxième partie du théorème est que si la taille initiale d'une région inflationnaire excède la distance de l'horizon (r > H-1), alors aucun événement extérieur à cette région ne peut entraver cette inflation, vu qu'aucune information concernant ces événements ne peut jamais l'atteindre. On peut considérer l'indifférences des régions inflationnaires pour ce qui se passe à côté comme une sorte d'égoïsme inoffensif : la croissance de la région inflationnaire dépend uniquement de ses vertus propre et non de celles du voisinage. Ce type de processus (inflation chaotique) conduit finalement à un univers de structure très complexe à des échelles énormes mais à l'intérieur de chaque région inflationnaire l'univers semble localement uniforme à un haut dégré.
Cet élément joue un rôle important dans toute discussion concernant les conditions initiales requises pour initier un processus inflationnaire ou pour rechercher la structure globale de l'univers.
[..] Autre remarque au sujet du rapport entre un univers de Sitter et un univers inflationnaire : beaucoup d'ouvrages sur la RG disent que l'espace de Sitter n'est qu'un espace statique. Comme nous l'avons montré précédemment, pourtant, l'espace décrit par la métrique ( 7.2.7 ) est géodésiquement incomplet, c'est à dire qu'il existe des géodésiques qui conduisent hors de l'espace ( 7.2.7 ). De la même façon, un observateur qui tombe dans un trou noir ne note rien d'exceptionnel durant son plongeon final à travers la sphère de Schwarzschild r = rg, ainsi dans un espace de Sitter quelqu'un situé au point initial r = r0 < H-1 émerge de cette région décrite par les coordonnées ( 7.2.7 ) après un temps propre fini. (Tandis que cela a lieu, un observateur stationnaire situé à r = ∞ dans une métrique ( 7.2.8 ) ou à t = 0 dans la métrique (7.2.7) ne doit pas s'attendre à voir son ami disparaître derrière l'horizon, mais il recevra de lui de moins en moins d'information. [..]
En l'absence d'observateurs, de matière, ou encore de particules de test, ce défaut de stationnarité est "sui generis" vu que les caractéristiques invariantes de l'espace de Sitter associé au tenseur de courbure sont indépendantes du temps. Ainsi, par exemple, la courbure scalaire de l'espace de Sitter est:
R = 12H2 = cte
Par conséquent, si l'univers inflationnaire était simplement un espace de Sitter vide, il serait difficile de parler de son expansion. Il sera toujours possible de trouver un système de coordonnées dans lequel l'espace de Sitter semble, par exemple, comme s'il était en contraction, ou comme s'il avait une taille H-1 (équations (7.2.5) et (7.2.7)).
Mais dans l'univers inflationnaire, l'invariance de de Sitter est ou bien brisée spontanément (du fait de la décroissance du vide de Sitter initial) ou bien brisée du fait d'une disparité initiale entre l'univers actuel et l'espace de Sitter. En particulier, le tenseur énergie-impulsion Tμν dans le scénario d'inflation chaotique, bien qu'il soit proche de
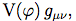 ne lui est jamais exactement égal, et dans les dernières étapes de l'inflation, l'ordre de grandeur du champs d'énergie cinétique
ne lui est jamais exactement égal, et dans les dernières étapes de l'inflation, l'ordre de grandeur du champs d'énergie cinétique 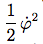
devient grand comparé à V(φ), et la différence entre Tμν et
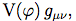 devient significative.
devient significative. La distinction entre un espace statique de Sitter et l'univers inflationnaire devient spécialement claire au niveau quantique, quand on analyse les inhomogénéités de densité
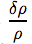 qui surviennent durant le temps de l'inflation.
qui surviennent durant le temps de l'inflation. Comme nous le montrerons dans la Sect. 7.5, à la fin de l'inflation, ces inhomogénéités croissent de
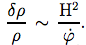
Ainsi, si le champs φ était constant et que l'univers inflationnaire ne pouvait être distingué d'un espace de Sitter, alors après l'inflation notre univers serait hautement inhomogène. En d'autres termes, un traitement correct de l'univers inflationnaire requiert que l'on ne prenne pas seulement en compte ses similitudes avec un espace de Sitter mais également ses différences, spécialement dans les derniers stades de l'inflation, quand la structure de la partie observable de l'univers fut formée.
  |
Page 1 sur 1 |
[ 1 message ] |
|
Qui est en ligne |
Utilisateurs parcourants ce forum : Aucun utilisateur inscrit et 3 invités |
| Vous ne pouvez pas publier de sujets Vous ne pouvez pas répondre aux sujets Vous ne pouvez pas éditer vos messages Vous ne pouvez pas supprimer vos messages Vous ne pouvez pas insérer des pièces jointes |
