Réaction aux propos de JP Luminet

Ce soir dans une émission sur la cinq, JP Luminet faisait une petite introduction à différents concepts topologie/astrophysique etc...

Suite à la présentation d'images du fond cosmologique, il en conclue que l'univers est fini (il semble assez catégorique égratignant au passage les cosmologistes qui croient encore à l'univers infini) car il manque des longueurs d'ondes, dans les fréquences, il compare la "finitude" de l'univers à la "finitude" d'une corde musicale incapable de restituer toutes la gamme.

Puis il continue en affirmant que la résonnance d'un "dodécaèdre de poincaré" aurait une résonnance très proche et que donc l'univers pourrait avoir cette topologie.

Le coup de l'univers fini suite à l'étude des images du fond cosmologique je ne l'avais jamais lu....

Voilà, vraiment sympa Luminet, c'est un plaisir de l'écouter.


Bon sinon, vous êtes tous en vacances ou quoi?

Depuis la présentation du modèle dodécaédrique avec faces interconnectées, qui est en soi marrant et intéressant, une controverse s'est installée depuis des années, car si ce modèle explique bien certaines données de l'observation du fond cosmologique (la faiblesse des fluctuations à grande échelle), d'une part d'autres explications de ces mêmes données sont possibles et d'autre part d'autres effets impliqués par le dit modèle n'ont pas été observés.

Dans cette situation il convient de considérer la vision de l'univers en forme de ballon de foot avec précaution : c'est une hypothèse parmi d'autres que l'observation n'a pas encore clairement sélectionné ni falsifié. On aura peut être du nouveau en 2008-2010 avec la mission Planck et ses mesures plus précises du fond cosmologique.

PS/ Certains sont en vacances, d'autres travaillent trop

OK.

On aurait donc une quasi sphère, que des impératifs mathématiques liés à la finitude de l'univers approcherait par la juxtaposition de plans (des pentagones par exemple) interconnectés entre eux (on passe d'un bout de l'univers à lautre).
Ces interconnections serait donc mathématiquement impossibles avec une sphère parfaite?
C'est marrant ça me rappelle plus une organisation cristalline de la matière qu'une organisation gravitationnelle sphérique, circulaire (planètes, soleils, galaxies etc..).

Concernant le dodécaèdre de poincaré JP Luminet n'était pas ausi affirmatif que pour la finitude de l'univers.
Il a dit que ce dodécaèdre "vibrait" d'une manière très proche de ce que l'on avait observé pour le fond diffus.

Et bon boulot à tous alors

LokiLeFourbe a écrit:

Ces interconnections serait donc mathématiquement impossibles avec une sphère parfaite?

Une sphère est aussi finie, et si l'on continue d'avancer tout droit on revient aussi au même point.

Mais une sphère est simplement connexe, ce qui signifie qu'il y a un seul parcours possible de lumière pour aller d'un point à un autre. Alors que dans un univers fini dont la topologie n'est pas simplement connexe, plusieurs parcours de lumière existent entre deux points et il serait donc possible de voir plusieurs copies des mêmes astres dans différentes directions du ciel.

Pour voir ces effets il y a ici un excellent logiciel.

Ouais..

Mais à ce niveau, les mathématiques ne sont elles qu'une extrapolation abstraite d'une réalité physique inconnue ou soupçonnée, un moyen intellectuel d'imaginer, de concevoir une réalité physique incompréhensible par nature.
C'est certainement mon faible (c'est peu dire) niveau en ce domaine, mais l'abstraction mathématique, me semble aussi inabordable et immatérielle, que l'abstraction théologique.

LokiLeFourbe a écrit:

Mais à ce niveau, les mathématiques ne sont elles qu'une extrapolation abstraite d'une réalité physique inconnue ou soupçonnée, un moyen intellectuel d'imaginer, de concevoir une réalité physique incompréhensible par nature.

Oui, mais lorsque les prédictions de la théorie sont confirmées par l'expérience, alors la théorie devient notre meilleure compréhension de la réalité, aussi absurde puisse elle paraître au premier regard.

Un exemple flamboyant est le modèle standard des particules, dont la structure mathématique est bien plus complexe que ces sphères de Poincaré. Pourtant, malgré l'apparente "immatérialité" d'une telle mathématique, elle décrit ce qu'il y a de plus matériel (la matière¹). Pour un aperçu d'une telle "théologie", voici le lagrangien du modèle standard:



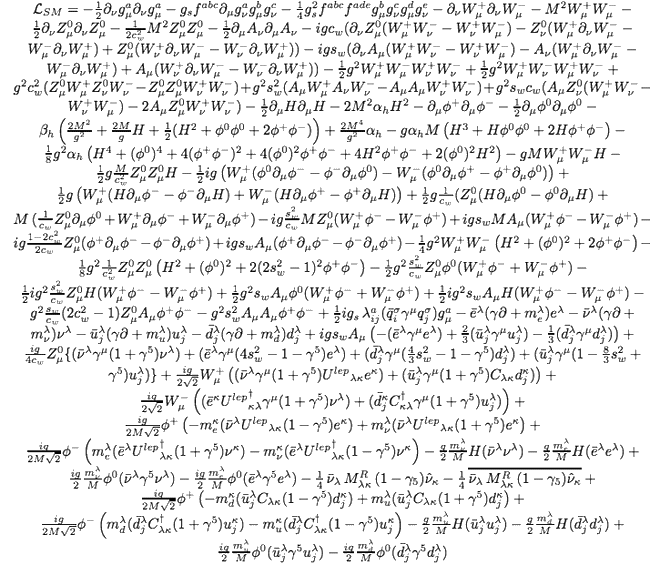
Bien sûr pour les modèles d'espace non simplement connexe dont on parlait plus haut aucune "image miroir" n'a été observée (c'est l'une des principales lignes de falsification) bien qu'on continue à les chercher. Mais si l'univers est fini mais très grand alors ces images miroir seraient au délà de l'horizon observable, donc leur absence n'exclut pas non plus la possibilité d'une telle topologie.

Enfin, il existe un nombre infini de topologies finies non simplement connexes. Si le modèle sphérique nous apparaît simple, parfait et préférable, il ne faut pas oublier que la Lune était aristoteliquement considérée une sphère parfaite jusqu'à que l'on voit au téléscope des énormes cratères sur sa surface, etc.

______
¹Matière que Platon considérait décrite par des cubes, tétraèdres, octaèdres et icosaèdres pour chacun des 4 éléments, réservant le dodécaèdre au 'dessin de l'univers'. Platon, Timée (360 aC)

"Haaaaa xantox m'a tuer"

Ta passion ne pourra combler mon ignorance, tu verras toujours au delà des nuages qui m'obscurcissent la vue, MAIS je fais confiance, car quand le savoir me manque, il me reste l'instinct et il m'incite au respect et à l'humilité.

Xantox, est ce que tu pourrais publier le code LaTex de l'équation ?

J'aimerais bien l'avoir, c'est sentimental

a+

Gilgamesh a écrit:

le code LaTex de l'équation

Le voici ainsi qu'une version PDF.

L'équation suit la notation de Martinus Veltman :

Bosons : A_μ, W_μ, Z⁰, g_μ
Quarks : u^κ, d^κ
Leptons : e^λ, ν^λ
Higgs : H, Φ⁰, Φ⁺, Φ^-
Masses : m_d, m_u, m_e, m_h, M_W
g=√4πα, g_s (interaction forte)
C_λκ : matrice de Cabibbo-Kobayashi-Maskawa
f^abc : constantes de SU(3)
Jauge de Feynman.
Les fantômes de Faddeev-Popov sont omis pour simplicité.

Merci xantox.

C'est dommage ça fait craquer le TeXer . Tu utilises quoi comme éditeur ?

a+

Il craque car c'est trop long, sinon tu peux utiliser le PDF. J'utilise l'excellent TeXMaker sur Mac mais qui existe aussi en version Windows et Linux, en version EN/FR et qui peut gérer des documents volumineux.

xantox a écrit:

Il craque car c'est trop long, sinon tu peux utiliser le PDF. J'utilise l'excellent TeXMaker sur Mac mais qui existe aussi en version Windows et Linux, en version EN/FR et qui peut gérer des documents volumineux.

Voila, j'allais te demander si c'était bien, merci.


a+

Celà inclut-il le cercle déférent (et les éventuelles épicycles) de la gravité ?

Par curiosité, que sont les "fantômes de Fadeev-Popov" ?

Heh, non il n'y a pas de gravité.

Les fantômes sont des champs fictifs introduits pour les besoins du calcul et qui disparaissent magiquement à la fin.

xantox a écrit:

Matière que Platon considérait décrite par des cubes, tétraèdres, octaèdres et icosaèdres pour chacun des 4 éléments, réservant le dodécaèdre au 'dessin de l'univers'.

Je connais un fanatique qui voit en Leibniz le précurseur du XML (entre autres bien sûr). Donc on peut voir en Platon le précurseur des groupes de Lie - et l'inverse. Et pour continuer dans le fétichisme, Alain Connes s'exprime informellement sur la phrase du modèle standard, ici & là.